在格密碼學中,我們經常會遇到一些計算困難的問題。這些問題的難解性是許多現代密碼系統安全性的基礎。簡單來說,這些問題就是找到一個隱藏在 格(Lattice) 中的秘密。
格在數學上可以被想像成是一個由一組**基向量(basis vectors)**透過整數線性組合所產生的點集合。舉例來說,在二維空間中,如果你有一組基向量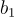 和
和 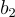 ,那麼格中的每一個點 v 都可以被表示為
,那麼格中的每一個點 v 都可以被表示為 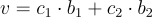 ,當中的
,當中的 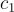 和
和 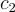 都是整數。
都是整數。
在格密碼學中,我們通常會遇到兩種情況:一種是「好」的基向量,它們彼此接近正交且長度都較短,可以很容易地找出格中的一些性質;另一種則是「壞」的基向量,它們彼此之間接近平行且長度很長,這使得在格中找到最短向量等問題變得非常困難。格密碼學的安全性正是建立在從「壞」的基向量來解決問題很難,但從「好」的基向量來解決問題相對容易的這種差異上。
基於格的密碼學中所依賴的核心計算困難問題。這些問題的安全性構成了整個密金鑰學領域的基石。
格上的計算問題通常分為兩大類:
最壞情況困難問題:這類問題是理論計算複雜性的核心,為密碼學的安全性提供了強有力的理論保證。
平均情況困難問題:這類問題直接作為密碼學原語(如加密、簽名)的建構基礎。它們的安全性可以歸約到最壞情況問題的困難性。
針對最壞情況困難問題下,會有以下2個計算問題:
1. 最短向量問題(SVP)
給定某個格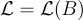 的任意基 B,找到一個最短的非零格向量,即滿足
的任意基 B,找到一個最短的非零格向量,即滿足 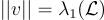 的
的 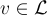 。
。
例子: 想像一個二維點陣,其基向量為 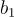 =(1,3) 和
=(1,3) 和 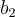 =(2,−1)。點陣中的向量可以是
=(2,−1)。點陣中的向量可以是 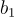 +
+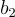 =(3,2)等等。而SVP 的目標就是在所有這些向量中,找出一個長度與原點的距離最短的一個。
=(3,2)等等。而SVP 的目標就是在所有這些向量中,找出一個長度與原點的距離最短的一個。
雖然這個2維例子是簡單,但當維度 n 增加時,SVP 就會變得極度困難。這就是為什麼它被視為一個NP-難問題。點陣密碼學的安全性正是建立在求解高維 SVP 的困難性上,即使是量子電腦也難以有效率地解決。許多基於點陣的密碼方案,例如 Gentry 的全同態加密方案(FHE),其安全性都直接與 SVP 的困難性相關。
2. 最近向量問題(Closest Vector Problem, CVP)
CVP 比 SVP 更進一步,它是在格之外給定一個目標向量 t,可以理解為某一個點,我們要找到格中距離這個目標向量最近的那個向量 v。給定一個格 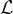 和一個向量
和一個向量 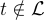 ,找到一個向量
,找到一個向量 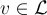 ,使得
,使得 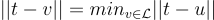
例子: 延續上面的二維格,現在給定一個目標向量 t=(1.5,2)。CVP 的任務就是在格 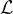 中找出一個點 v,使得 v 到 t 的距離 ||t−v|| 最小。
中找出一個點 v,使得 v 到 t 的距離 ||t−v|| 最小。
CVP 是一個更廣泛的問題,因為 SVP 實際上是 CVP 的一個特例。當目標向量 t 設定為原點 (0,0,…,0) 時,CVP 就變成了 SVP。CVP 在密碼學中應用廣泛,例如 NTRU 加密方案 的解密過程就可以被視為一個 CVP 問題。如果攻擊者能夠有效率地解決 CVP,他們就能夠破解 NTRU。
